Según la mecánica clásica, ya sea la de Newton o la relativista, si colocamos un sistema de inercial, con el átomo en reposo, el electrón queda descripto a través de su TRAYECTORIA CONTINUA: r(t)=(x(t), y(t), z(t)). En este caso, OBSERVABLES podrían ser la misma trayectoria r(t) y el momento lineal p=mv (donde v es la velocidad, primera derivada temporal de r(t)). El canónico (r(t), p) determina, en la física clásica, completamente el estado del sistema, es decir, toda la información dinámica de la partícula se puede calcular una vez obtenidos los valores del par canónico (por ejemplo la energía total es E=p^2/2m + V(r)).
Ahora, el núcleo positivo genera un campo eléctrico que realiza un fuerza sobre el electrón. Utilizando la noción de trayectoria, podemos escribir la segunda ley de Newton, que establece que la fuerza es proporcional a la aceleración (que es la segunda derivada temporal de r(t)): F=ma, para este caso -e.grad V=e.E=ma, donde V es el potencial electrostático del núcleo. Según las ecuaciones clásicas del electromagnetismo, las ecuaciones de Maxwell, el campo E está determinado por la distribución de carga del núcleo (en este caso es muy simple: el núcleo se considera una carga puntual y por lo tanto el potencial que genera es V(r)=k/r ). En resumen, el electrón es atraido al núcleo por una fuerza eléctrica.

Resolviendo la segunda ley de Newton para este caso se puede obtener, por ejemplo, una órbita circular (aquí la solución exacta de las ecuaciones de movimiento para este caso http://en.wikipedia.org/wiki/Kepler_problem ). Sin embargo, esto no tiene en cuenta un efecto: una carga acelerada emite ondas electromagnéticas ("luz".) las cuales se "llevan" energía del sistema. El electrón orbitante ciertamente está acelerado, por lo tanto debe emitir ondas em. Estas ondas le "quitan" energía al sistema.
Para la órbita circular, la energía total es E (prop.) 1/r y la potencia a la cual radía el electron es P=dE/dt (prop.) a^2 (fórmula de Larmor). Entonces, por la conservación de la energía, la tasa a la cual el electrón emite energía debe ser igual a la tasa a la cual el sistema pierde energía, es decir cte. d/dt(1/r)=cte´.a^2. Como a es la segunda derivada de r, lo anterior es una ecuación diferencial que nos va a dar como se modifica el radio de la órbita circular a causa de que el electrón emite energía en forma de ondas em. El resultado es una función r(t) DECRECIENTE en el tiempo, es decir, ¡CLASICAMENTE, EL ELECTRON SE PRECIPITA EN ESPIRAL HACIA EL NULCEO!. Con lo cual, ¡el átomo clásico es inestable!.
(mientras se precipita hacia el nucleo, la velocidad angular del electron aumenta y como la frecuencia de la onda em que emite es directamente proporcional a la velocidad angular esto implica que, cuando llega al nucleo, el electrón emitio ondas en todas las frecuencias del espectro, es decir, se veria que el atomo clasico emite en un espectro continuo
Acá hay un problema para la clásica...¡experimentalmente se observa que los átomos son estables!, entonces o está mal Newton o Maxwell... o ambos. Resulta que ambas teorías clásicas están erradas, al menos en el mundo subatómico. El principal colapso es el de la teoría de la mecánica clásica, la cuántica cuestiona la noción misma de trayectoria, que es fundamental en la segunda ley de Newton ya que permite definir nociones como velocidad y aceleración. Como en la fórmula de Larmor entra a, es claro que no puede ser válida a nivel cuántico. Y entonces, ¿qué hacemos?¿se murió la física?. Bueno, técnicamente, si, se murió la clásica al menos. Por suerte, surgieron una serie de experimentos que permitieron elaborar una nueva teoría que reemplazaría, exitosamente, a la ya moribunda teoría newtoniana. Y si, esa nueva teoría es la famosa... ¡mecánica cuántica!. Pero, ¿qué es la mc y por qué tiene fama de ser tan poco intuitiva y misteriosa?. Antes de adentrarnos en territorio enemigo, más vale que tengamos las armas matemáticas bien afiladas, asi que, sin más preambulos, ¡los divertidísimos vectores!:
Hay dos formas de definir los vectores: la primera, y más fundamental, es la algebraica (ver axiomas de definición en http://en.wikipedia.org/wiki/Vector_space); la segunda, es la geométrica. Veremos ahora esta última. Los números reales R son los números de la recta real, valga la redundancia. Por ejemplo: 1, 2.34597, pi, raíz de 2, etc. El producto cartesiano "x" de R con R, RxR=R^2, nos da un par ordenado de números reales v=(x,y), donde x e y son números reales. Este par ordenado puede verse como un par de coordenadas que podemos graficar en un sistema cartesiano de ejes ortogonales:

Si trazamos una recta que une el origen con el punto v del plano, este segmento orientado es un vector geométrico, que además está caracterizado algebraicamente por el par ordenado v=(x,y). Definiendo la suma de dos vectores v1 y v2 como el nuevo vector v=(x1+x2, y1+y2), y el producto por un escalar..., llegamos a que estos vectores geométricos que definimos verifican, a través de la caracterización algebraica que mencionamos, la definición algebraica de vector. ¿Para qué sirven estos vectores?, básicamente, todos estos vectores "viven" en R^2 (a lo bestia, el plano) y sirven para, de nuevo a lo bestia, indicar o caracterizar "direcciones" en ese plano. Por ejemplo, si el origen está en una esquina y un taxista te pregunta ¿maese, donde queda la calle x (eje x)?, entonces, si el eje y coincide con la dirección de la calle en la cual circula el taxi (decreciendo su valor de y, pero con y>0), uno le puede contestar: siga la dirección del vector (1,0), que es paralelo a la calle x, ud está actualmente en la dirección y sentido del vector (0,-1).
Los vectores tienen la propiedad básica de que se pueden "descomponer" como suma de otros vectores. Por ejemplo, el vector (1,2) se puede escribir como una combinación lineal (1,2)=1.(1,0)+2.(0,1). El conjunto de vectores {(1,0),(0,1)} se llama una "base" de R^2. En la física, ejemplos de vectores son la velocidad, la aceleración, el campo eléctrico, etc. Es decir, para todas estas cantidades, no basta con solo dar su "intensidad", sino que también hay que especificar la dirección. Ahora ya tenemos las armas matematicas listas para darle pelea, quizas hasta la muerte, a la mc.
Veamos en que consiste el experimento de Stern-Gerlach:
El movimiento "giratorio" de un cuerpo se describe mediante un vector L perpendicular al plano donde está contenido el movimiento, se llama momento angular, es parecido al momento lineal solo que este es angular jeje ( si no actuan fuerzas externas, el momento lineal se conserva; si no actuan torques externos, el momento angular se conserva, es decir, su valor permanece constante):

Imaginemos que lo que gira es un electrón. Por culpa de la carga elétrica del mismo, hay además un momento magnético dipolar orbital que se calcula a partir del momento angular del electrón:

Por ejemplo, un imán común y corriente es un dipolo magnético. Cuando acercamos el imán a un campo magnético, este se mueve, es decir que se produce una fuerza (y un torque también). Entonces si colocamos el electrón que gira en un campo magnético externo B(no estamos hablando del núcleo ahora), va a haber una fuerza Fz=uz dBz/dz, para el siguiente esquema:
Es decir, los átomos salen de la fuente y se desplazan por el eje y, se encuentran con un campo magnético (inhomogéneo) en la dirección del eje z, esto produce una fuerza, también en la dirección del eje z (ver ecuación anterior) que provoca que los átomos, inicialmente en un haz, se "dispersen" sobre el eje z, como muestra la figura en "classical prediction". Veamos la fórmula de nuevo Fz=uz dBz/dz, con u (prop.) L. En principio, los electrones pueden girar como se les de la gana, entonces L toma todo un espectro contínuo de valores. Esto implica que u también toma un espectro contínuo de valores y por lo tanto hay también un espectro contínuo de valores de fuerza, con lo cual obtenemos la imagen clasica con los átomos formando una franja contínua sobre el eje z. Sin embargo, como se indica en la gráfica, ¡esto no es lo que se ve en la realidad, solo se registran dos haces!. Esto implica que solo hay dos valores de fuerza y por lo tanto dos valores de uz y por lo tanto, finalmente, solo dos valores permitidos de Lz ( en realidad de Sz, que es el spin, un momento angular intrínseco, el L en este caso es cero, pero el spin es un tipo de momento angular al fin y al cabo, y tiene su propio momento magnetico de spin, etc.). Se dice entonces que la componente z del spin S está CUANTIZADA, esto en contraposición a la clásica que solo permite espectros continuos para este tipo de observables. Esto es una peculiaridad propia de la cuántica: en esta, en general todos los observables que clásicamente son contínuos (como la energía, el momento lineal y angular, ¡la posición!, etc.) pueden estar cuantizadas. Los valores "cuánticos" que puede tomar Sz son:
Sz=(cte. de planck sobre 2pi).ms, donde ms=+1/2 o -1/2.
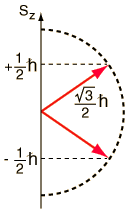
(únicas dos posibles orientaciones del spin; el módulo de S, la "longitud" del segmento orientado, es raíz(3)/2.h/2pi, como raíz(3)/2 es mayor que 1/2, entonces el vector S nunca se alinea completamente con el eje z)
De por sí, esto es bastante extraño ya, pero sigue...
Pongamos varios aparatos de Stern-Gerlach sucesivamente ("experimentos secuenciales":
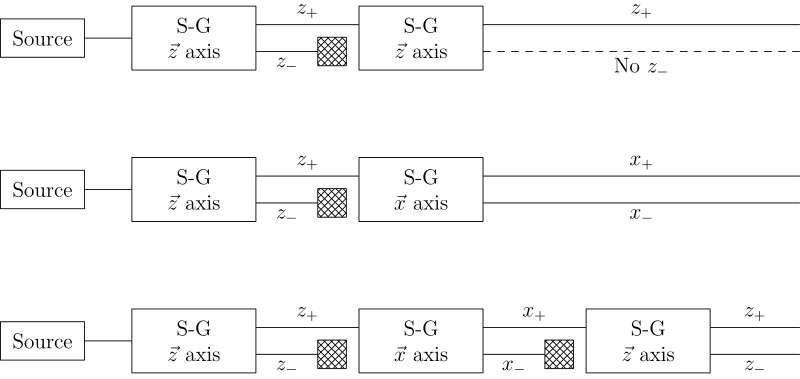
Nos concentremos en el último de los experimentos. Del primer aparato, salen los átomos con spin S=(Sx, Sy, cte.1/2) oS=(Sx, Sy, -cte.1/2). Se bloquea la S=(Sx, Sy, -cte.1/2), por lo que todos los átomos que llegan al segundo aparato tienen spin S=(Sx, Sy, cte.1/2). Del segundo aparato, salen con spin S=(cte.1/2, Sy, Sz) o S=(-cte.1/2, Sy, Sz). Se bloquea S=(-cte.1/2, Sy, Sz), por lo que todos los átomos que llegan al tercer aparato tienen spin S=(cte.1/2, Sy, Sz). Ahora, ¡sorpresa!: del tercer aparato, los átomos salen con spin S=(Sx, Sy, cte.1/2) o S=(Sx, Sy, -cte.1/2). ¿cómo puede ser, si al salir del primer aparato habíamos anulado los átomos con spin S=(Sx, Sy, -cte.1/2)?¿de donde se "regeneró" este valor de spin?. Clásicamente, si eliminamos S=(Sx, Sy, -cte.1/2), este valor no puede volver a aparecer, ya que despues nos concentramos en Sx, que no tiene nada que ver. En cierto sentido, la medición de Sx, anula todo lo que se había hecho antes sobre Sz. Se dice que Sz y Sx son observables "incompatibles". Pero... ¿como damos sentido a todo esto?¿como armamos una teoría con todo esto?. "Sencillo": clásicamente, el estado del sistema está caracterizado por el par canónico (r(t), p), donde r(t) y p son funciones CONTINUAS. Pero ya vimos que, a nivel subatómico, p, por ejemplo, no es continuo, "salta" de un valor a otro y vuelve a un dado valor a pesar de que se elimine inicialmente al valor en cuestión y no se vuelva a "tocar" nada en esa dirección. En clásica, los valores numéricos que toman r(t) y p y el estado del sistema son la misma cosa, es decir, basta dar los valores de esas funciones para caracterizar el estado del sistema. Sin embargo, esto no funciona en cuántica. En mc, separamos lo que es el estado del sistema por un lado y los que son los valores numéricos de los observables por el otro. Los estados cúanticos de un sistema se representan mediante un vector "ket" |e>, que pertenece a un espacio vectorial abstracto H (es decir, no lo traten de "visualizar".) Los observables como la energía, el momento, etc., se representan como operadores lineales A:H a H, es decir que A actuando en el ket |i> da otro ket |f>, A|i> =|f>. Los kets |a´> tales que A|a´>=a´.|a´> se llaman autokets de A y los números a´ sus autovalores asociados. Los autokets de los operadores que representan observables físicos forman una base de H. Entonces, el postulado fundamental de la mecánica cuántica es el siguiente:
SUPONGAMOS QUE EL SISTEMA ESTA INICIALEMTE EN EL ESTADO |e>. COMO LOS AUTOKETS {|a´>} DE A FORMAN UNA BASE, ENTONCES SE PUEDE HACER LA DESCOMPOSICION [e>=C´|a´>+C´´|a´´> (con H bidimensional para simplificar). CUANDO MEDIMOS (INTERACCIÓN ENTRE MUNDO MACROSCÓPICO CON EL MICROSCÓPICO, LA MECÁNICA CUÁNTICA ESTABLECE QUE LA NOCIÓN DE LO "PEQUEÑO" Y LO "GRANDE" ES REAL Y ABSOLUTA) EL OBSERVABLE A, LO UNICOS VALORES ADMISIBLES QUE SE PUEDEN PRESENTAR SON LOS AUTOVALORES a´ DE A. LA MC DICE QUE LA PROBABILIDAD DE MEDIR a´ ES |C´|^2 Y, SI SE MIDE ESTE VALOR, EL ESTADO DEL SISTEMA COLAPSA DE |e> HACIA |a´>.
Veamos que estos postulados explican lo observado en los experimentos secuenciales de Stern-Gerlach. Los observables en este caso son Sz y Sx. Cuantizamos el sistema "elevando" el "status" de Sz y Sx de funciones clásicas a operadores cuánticos. Los autovalores de Sz son +h/2pi.1/2 o -h/2pi.1/2 (h es la cte. de planck) y los autovalores de Sx también son +h/2pi.1/2 o -h/2pi.1/2. Asociado al autovalor +h/2pi.1/2 de Sz está el autoket |Sz+> y asociado al autovalor +h/2pi.1/2 está el autoket |Sz->. De forma análoga para Sx. Como los observables son incompatibles, los |Sz+/-> forman una base y los |Sx+/-> forman otra base independiente. Cuando los átomos salen del primer aparato están en el estado |e>=|Sz+>=C(+)|Sx+>+C(-)|Sx->. El aparato SGx "mide" el observable Sx. Luego el estado |e>, que estaba inicialmente en |Sz+>, colapsa a |Sx+> o a |Sx->. Se bloquea el canal para |Sx-> y por lo tanto el estado al salir del segundo aparato es |e>=|Sx+>. Ahora, |Sz+/-> forma una base, entonces |e>=|Sx+>=k(+)|Sz+>+k(-)|Sz->. El tercer aparato, de tipo SGz, mide Sz. Entonces, al medir Sz en el tercer aparato, el estado |e>, inicialmente en |Sx+> al salir del segundo aparato, puede colapsar tanto a |Sz+> COMO ASI TAMBIEN A |Sz->, ya que ambos son los vectores que forman la base en la cual es descompuesto |e>=|Sx+>.
Si llegaste hasta acá, ¡razonando!, entonces podés afirmar EN SERIO que entendés la mecánica cuántica en todo su "esplendor".
Para que veas la diferencia con la clásica: el oscilador armónico.

La fuerza que el resorte ejerce sobre la bolita es F=-k.x, entonces la segunda ley de newton, f=m.a, es -k.x=m.d^2 x/dt^2, recordando que la aceleración es la segunda derivada temporal de x. Queda un ecuación diferencial. La solución es x(t)=xi.cos(wt), con w=raíz(k/m) y xi la amplitud inicial. La energía total es la potencial 1/2kx^2 más la cinética 1/2mv^2=p^2/2m, E=1/2kx^2+1/2mv^2=1/2k(xi)^2. Ahora queremos resolver el sistema cuanticamente. Cuantizamos el sistema elevando x y p a operadores (se demuestra que obedecen la regla de conmutación [x, p]=xp-px=i.h/2pi). Como la energía depende de x y p, entonces también se transforma en un operador. Con un cálculo un poco tedioso se llega a que la energía del oscilador está cuantizada, siendo los autovalores En=h/2pi.w(n+1/2), con n=0,1,2,... . La posición de la partícula también es un observable y por lo tanto se puede calcular la probabilidad de hallar a la partícula en un dado valor de x, el resultado es:

(rojo es mucha probabilidad, negro es probabilidad nula)
La probabilidad depende del nivel de energía. En el segundo nivel, por ejemplo, ¡hay probabilidad de encontrar a la partícula en los extremos pero en el centro la probabilidad es nula! ¡¿cómo hace para pasar de un extremo a otro si nunca puede pasar por el centro?!...misterios de la cuántica... .
Aplicando el formalismo anterior al electrón orbitante en un núcleo atómico se obtienen reultados similares: la energía, el momento angular y la posición están cuantizados, por ejemplo (ver http://en.wikipedia.org/wiki/Hydrogen_atom). Lo interesante es que al cauntizar el campo electromagnético (la electrodinámica cuántica), se ve que el campo en realidad está compuesto por partículas, los fotones, cada uno de energía E=hf, donde f es la frecuencia de la onda. También se demuestra con la electrodinámica cuántica que si el electron está en uno de los niveles de energía, entonces puede permanecer en el mismo y no radía (con lo cual el átomo cuántico es estable; según la clásica, tendría que empezar a radiar inmediatamente y decaer). Cuando decae de un nivel Ei a otro Ef, ya sea por decaimiento espontáneo (después de un tiempo de vida finito en un nivel exitado, el electrón decae a otro más "estable".) o estimulado, emite un foton, de frecuencia f=(Ei-Ef)/h, en el proceso. Como E está cuantizada, esto implica que solo se emitirán fotones de algunas frecuencias solamente y no un espectro continuo, como un arcoiris (esto se vería en el átomo clásico). El resultado son los, experimentalmente medidios, espectros de líneas espectroscópicos:
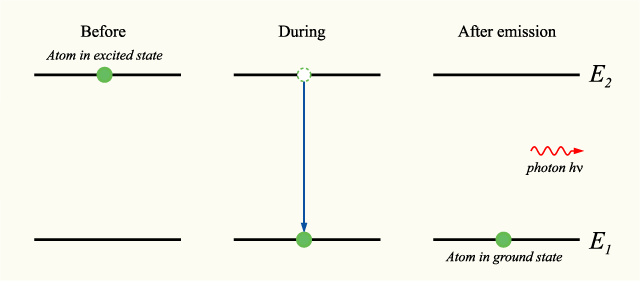
Luego, separamos con un prisma los distintos colores de los cuales está compuesto el haz de luz total que emite el átomo:

Proyectando en una pantalla vemos:

(Espectro de emisión del Hidrógeno) En esta foto literalmente estás "viendo" a la cuántica (es decir, sus efectos son muy obvios). Se ven lineas de varios colores porque no todos los atomos del gas tienen las mismas transiciones, es decir, el elctron en un atomo puede decaer del segundo al primer nivel, mientras que en otro, el electron puede decaer del tercero al segundo, los fotones en estos casos tienen diferente energia, y por lo tanto distinta frecuencia ("el color".

Probablidad de encontrar al electrón en el átomo de Hidrógeno, en el centro está el núcleo (de arriba a abajo, los distintos niveles de energía; de izquierda a derecha, los distintos valores para el módulo de L).



No hay comentarios:
Publicar un comentario